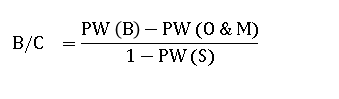ENGINEERING ECONOMY
Engineering economy is calculating, estimating, and assessing the projected economic implications of options meant to achieve a certain goal. Mathematical approaches make it easier to evaluate economic options.
Engineering Economics is a critical subject for engineers. This topic helps students comprehend the need of economic information in order to be an effective manager and decision maker.
Economic concepts are utilized to make business decisions in an unpredictable and changing business environment. Economics theories cover topics such as demand, price, cost, production, competition, trade cycles, and national income, and others.
Engineering economics is concerned with the systematic assessment of the economic advantages of proposed engineering solutions. Engineering economics is concerned with technical analysis with a focus on economic factors, with the goal of helping decision-making.
Engineering economics and conventional microeconomics are closely related. It is concerned with operational issue solving and decision making. Thus, “Engineering Economics” refers to “the parts of economics and their analytical tools that are most important to the engineer’s decision-making process.”
The seven-step methods used to support decision making are as follows:
1. Identifying, defining, and evaluating the issue.
2. Look for options that are both prospective and realistic.
3. Including the fundamental cash flow method.
4. The decision should promote the organization’s long-term interests.
5. Examining the economic elements of the engineering problem:
6. The preferable option is determined by the total effort.
7. Take special care to ensure feedback is given for operational improvements.
Interest
Interest is the amount of money paid for the use of borrowed capital (from the borrower’s perspective) or the revenue generated by money loaned (from the lender’s perspective).
F= P+I
Simple Interest
In simple interest, just the initial principle bears interest, and the amount of interest to be paid changes directly with time.
The simple interest formula is as follows:
I = Prt
The future amount is
F= P + I
F= P + Prt
Where
I = interest
P = principal, present amount, capital
F = future amount, maturity value
r = rate of simple interest expressed in decimal form
t = time in years, term in years
Ordinary and Exact Simple Interest
When the time t is specified in days, the fractional part of the year is computed with a denominator of 360, 365, or 366. The denominator in ordinary simple interest is 360, but the denominator in precise simple interest is either 365 or 366. As a result, we might argue that ordinary interest is bigger than precise interest.
Ordinary simple interest is calculated using the banker’s year.
Banker’s year
- Year = 12 months
- 1 month = 30 days (all months)
- 1 year = 360 days
The actual number of days in a year is used to calculate exact simple interest. One year consists of 365 days in the regular year and 366 days in the leap year. A leap year is one in which the month of February is 29 days long, as opposed to an ordinary year in which the month is only 28 days long. Every four years, a leap year is observed.
If d is the number of days in a month, then…
In ordinary simple interest.
- t = d/360
In exact simple interest
- t = d/365 ( for ordinary year)
- t = d/366 (for leap year)
COMPOUND INTEREST
In compound interest, the interest earned by the principal at the conclusion of each interest period (compounding period) is added to the principal. The whole (principal + interest) will earn interest again in the following compounding period.
Elements of Compound Interest
P = principal, present amount
F = future amount, compound amount
i = interest rate per compounding period
r = nominal annual interest rate
n = total number of compounding in t years
t = number of years
m = number of compounding per year
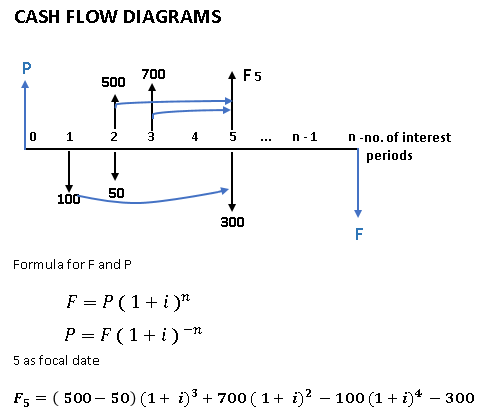
Cash flow
The amount of money documented as revenues or disbursements in a project’s financial documents.
A cash flow diagram depicts the flow of cash as arrows on a time line scaled to the amount of the cash flow, with costs represented by downward arrows and receipts represented by upward arrows. Year-end convention costs incurred during the year are presumed to be incurred at the conclusion of the year.
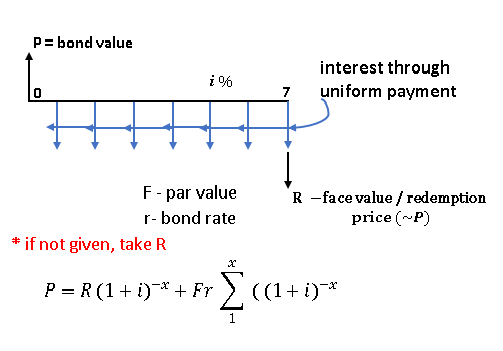
Bonds
Certificates of indebtedness
Bond Value-present worth of all future amounts that are expected to be received through ownership of a bond
Discount
A discount is the difference between the future worth of a certain commodity and its present worth. There are two kinds of discounts: A trade discount is a discount offered by a seller in order to encourage trading. A cash discount is a decrease in the selling price given to entice a buyer to pay immediately.
D = F – P
Annuities and Capitalized Cost
Annuity
An annuity is a series of payments that are made at regular periods. Annuities include financial activities such as installment payments, monthly leases, life insurance premiums, and monthly retirement benefits.
Elements of Annuity
A = amount of periodic payment
P = present amount of all periodic payments
F = future worth of all periodic payments after the last payment is made
i = interest rate per compounding period
n = total number of payments
m = nominal rate (see compounded interest)
t = number of years
Types of Annuities
ORDINARY ANNUITY
Payment are made at the end of each period.
The future amount F in the cash flow diagram above is the sum of payments from the end of the first period to the end of the nth period. Take note that the total number of payments is n, as is the total number of compounding periods. As a result, the number of payments and the number of compounding periods in a regular annuity are identical.
Future amount of ordinary annuity, F
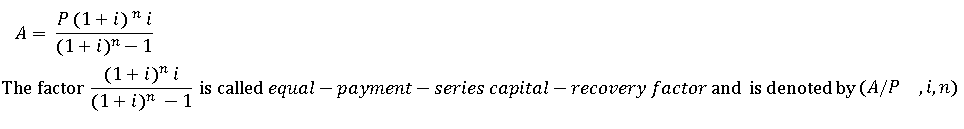
Present amount of ordinary annuity, P
Periodic payment of annuity, A
Value of A if F is known:
Value of A if P is known:
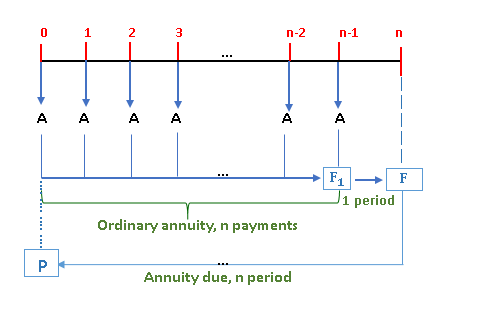
ANNUITY DUE
Payments are made at the beginning of each period.
F1 is the total of n ordinary annuity payments, as shown in the diagram above. F1 is one compounding period away from the future amount of annuity due at the end of the nth period. In symbol, F = F1 (1 + i).
Future amount of annuity due, F
Present amount of annuity due, P
DEFERRED ANNUITY
Payment id deferred a certain number of period.
The first payment was made at the end of the kth period, and a total of n payments were paid, as shown in the diagram. As seen in the diagram, the n payments generate a regular annuity.
Future amount of deferred annuity, F
Future amount of deferred annuity, F
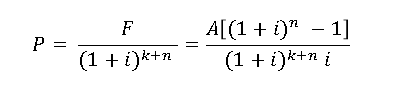
PERPETUITY
Whose payment continue forever.
There is no definite future in perpetuity, thus, there is no formula for the future amount.
P is the current amount of perpetuity
From the current value of the ordinary annuity:
Arithmetic Gradient
Arithmetic gradients change by the same amount each period.
Geometric Gradient
Geometric gradients change by the same percentage each period.
DEPRECIATION
Depreciation is the decrease in the value of physical properly (except land) with the passage of time.
Book Value: the value of property as recorded in an enterprise’s accounting records.
Salvage/Resale Value: the amount earned from the sale of a property after it has been utilized.
Scrap Value: the amount of money that a piece of property would sell for if it were thrown away.
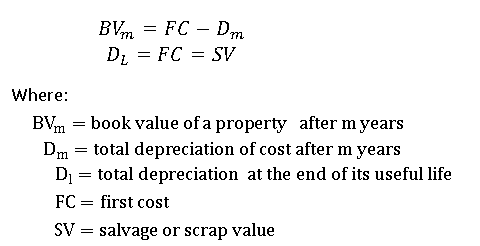
Types of Depreciation
1.Straight-Line Method
A method based on the assumption that the decrease in value is exactly proportionate to the property’s age
Straight Line Method Formula:
2.Declining Balance
The declining balance method assumes that the yearly cost of depreciation is a set percentage (k) of the salvage value at the start of the year.
Note: This method is not applicable if there is no salvage value.
3. Double Declining Balance Method
A method similar to the declining balance method in which the rate of depreciation k is substituted by 2/L.
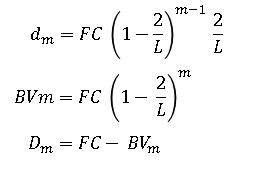
4.Sum-of-the-Year’s-Digits (SYD)
The sum-of-the-year’s-digits method also provides for accelerated depreciation. To begin, combine all of the digits from the asset’s projected life.
Sum-of-the-years-digits method formula:
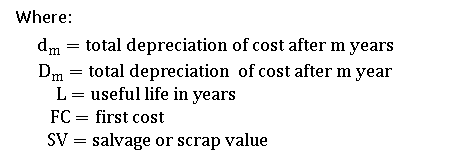
4.Sinking Fund Method
The Sinking Fund Method is based on the assumption that a sinking fund has been established in which cash will accumulate for replacement. The whole amount of depreciation that has occurred up to that point is presumed to be equal to the cumulative amount in the sinking fund at that time.
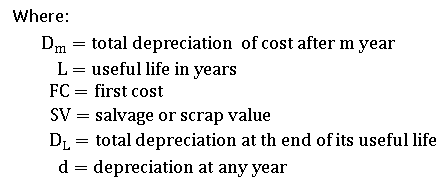
5.Units-of-Production Method
The units-of-production depreciation method depreciates assets during their useful life based on the total number of hours utilized or the total number of units to be generated by using the asset.
Units-of-Production Method Formula:
Break-Even Analysis
Calculate when revenue equals cost, or when one alternative equals another if both are dependent on the same variable.
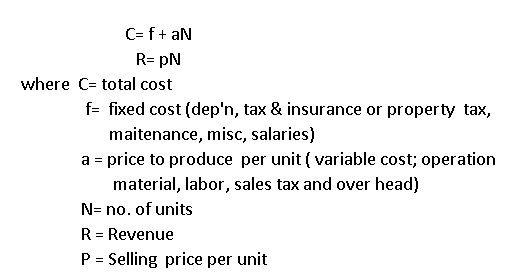
Inflation
Inflation is defined as an increase in the price of goods and services from one year to the next, reducing money’s buying power.
If the uninflated present value is to be calculated,
Benefits -Cost Ratio Method
Benefits-Cost Ratio-refers to a financial measurement that helps in determining the feasibility of a proposed project based on its anticipated costs and benefits. To put it another way, the ratio defines the link between the predicted added gain from a project and the expenditures associated with its completion.
The B/C ratio is defined as the ratio of the equivalent worth measure applied can be present worth, annual worth, or future worth.
Conventional B/C ratio with PW
Where: PW = present worth
B= benefits of proposed project
1= initial investment in the proposed projects
O & M= operating & maintenance costs of the proposed project
Modified B/C ratio with PW:
Conventional B/C ratio with AW
Modified B/C ratio with AW:
Conventional Benefits Cost Ratio with PW, Salvage value (S)
Modified Benefits Cost Ratio with PW, Salvage value (S)
