TRIGONOMETRY FORMULAS
Trigonometry is a field of mathematics dealing with particular angle functions and their application to computations. There are six fundamental trigonometric ratios that are utilized in all trigonometric formulae. These ratios are also known as trigonometric functions since they make extensive use of trigonometry formulae. Sine, cosine, secant, cosecant, tangent, and cotangent are the six fundamental trigonometric functions.
The right-angled triangle is used to generate trigonometric functions and identities. When we know the height and base side of a right triangle, we may use trigonometric formulae to calculate the sine, cosine, tangent, secant, cosecant, and cotangent values.
A right-angled triangle has three sides: the hypotenuse, the opposite side (perpendicular), and the adjacent side (base). The longest side is referred to as the hypotenuse. The perpendicular is the side opposing the angle, and the adjacent side is the side on which both the hypotenuse and opposite side rest.
BASIC TRIGONOMETRIC FORMULAS
In Trigonometry, there are six ratios that are utilized to find the elements. They are referred to as trigonometric functions. Sine, cosine, secant, co-secant, tangent, and co-tangent are the six trigonometric functions.
The trigonometric functions and identities are obtained using a right-angled triangle as a reference.

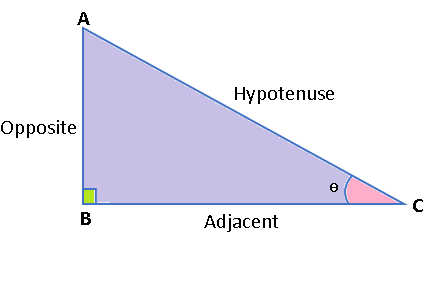
The sine, cosine, tangent, secant, cosecant, and cotangent values of a right triangle may be calculated using trigonometric formulae if the height and base side of the right triangle are known. Using trigonometric functions, the reciprocal trigonometric identities are also obtained.
TRIGONOMETRY TABLE
The table below contains trigonometric formulae for angles that are widely utilized in problem solving.
| Angles in Degrees | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| Angles in Radians | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | π2 |
| sin | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 | |
| cos | 1 | √3/2 | 1/√2 | 1/2 | -1 | 1 | ||
| tan | 1/√3 | 1 | √3 | ∞ | ∞ | |||
| cot | ∞ | √3 | 1 | 1/√3 | ∞ | ∞ | ||
| csc | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
PERIODICITY IDENTITIES IN DEGREES. Shifting angle by by π/2, π, 2π, 3π/2 (Co-Function Identities)
| sin (π/2 – A) = cos A | cos (π/2 – A) = sin A |
|---|---|
| sin (π/2 + A) = cos A | cos (π/2 + A) = – sin A |
| sin (3π/2 – A) = – cos A | cos (3π/2 – A) = – sin A |
| sin (3π/2 + A) = – cos A | cos (3π/2 + A) = sin A |
| sin (π – A) = sin A | cos (π – A) = – cos A |
| sin (π + A) = – sin A | cos (π + A) = – cos A |
| sin (2π – A) = – sin A | cos (2π – A) = cos A |
| sin (2π + A) = sin A | cos (2π + A) = cos A |
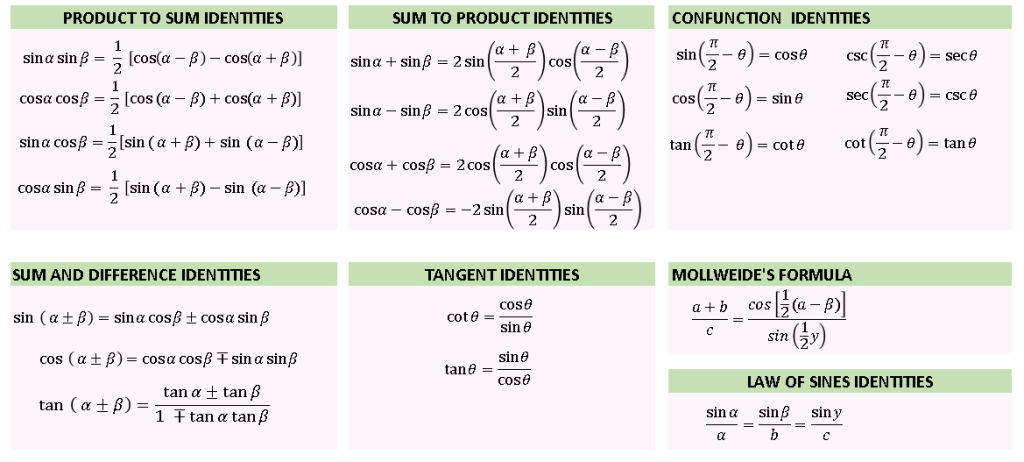
TRIGONOMETRY : LAWS AND DENTITIES